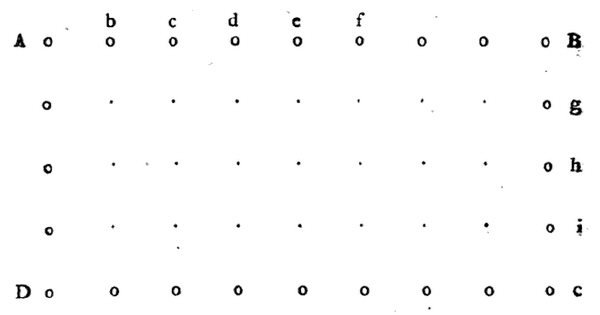
Hoedanig men in het vierkant plant? Uit Beschouwende en werkdadige hovenier-konst (1753), Johann Hermann Knoop
Ik weet niet goed wat ik wil zeggen, hoe het te zeggen, waarom ik het wil zeggen en wat ik er mee wil zeggen. Onduidelijk? Zeker te weten. Volgt een vluchtige zinloze gedachte? Mogelijk.
De titel geeft het veld al aan: plantafstanden. Zie ook eerdere berichten en reacties op onze weblog: 11 nov 2015, 18 juli 2015, 6 jan 2014.
Historische plantafstanden (zeg voor 1820) waren in voeten of roeden, en dan neem ik voor het gemak even de Rijnlandse Roede en laat ik al die anderen en de onderlinge verschillen even achterwege. Laten voor het gemak een plantafstand van 1 roede = 12 voeten = 3,767 meter nemen, en dan noemen we dit ‘standaard’ plantafstand. In meters roept dat aantal cijfers achter de komma roept iets op van dat kan niet, dat doe je niet. Stel je constateert dat een laan een plantafstand van 12 voeten had. Kan iemand zo’n laan herstellen en de bomen op 3,767 m zetten? Lijkt me niet. Ergens botst dat ‘oude’ afgeronde met gemak te gebruiken getal in voeten/roeden met de haast onmogelijke nauwkeurigheid in de ‘nieuwe’ eenheid meters. Terwijl beide tegelijkertijd voor hetzelfde staan. Stel er was nooit sprake geweest van roeden en voeten, maar direct van meters, zou er dan ooit een ‘standaard’ plantafstand van 3,767 m zijn geweest? Denk het niet. Als je bovenstaande doortrekt naar het ontwerp, naar de ontwerptekening, dan doet de maateenheid er waarschijnlijk minder toe. Het gaat dan meer om verhoudingen; 1-2, 3-4 enz.
Wat wil ik hier nu mee zeggen? Dat weet ik eigenlijk niet, heb alleen iets van het ‘schuurt’.
Tot nu gaat het eigenlijk alleen maar over het ideale plaatje, over de ‘standaard’, maar er is ook nog zoiets als het ‘gegevene’, het terrein, met zijn mogelijkheden, beperkingen en onmogelijkheden. En dan kom je tot afwijkingen ten opzichte van de ‘standaard’, of positiever gezegd tot iets als ‘verdeling met benadering van de standaard’. Johann Hermann Knoop geeft een voorbeeld in zijn Beschouwende en werkdadige hovenier-konst (1753). Bij een laan dient eerst de plaats van de eerste (A) en de laatste boom (B) bepaald te worden. De distantie tussen beiden dient vervolgens gemeten te worden: ‘Ik stel B.V. dat de lengte AB 132 voeten was, en dat de bomen circa 16 voeten van malkander sullen staan, dan segt per divisie 16 in de 132 hoeveel maal? Komt 8. Distantie tussen A en B, dat is dat ‘er 9 bomen in die rey komen; maar daar schieten van de 132 voeten 4 voeten over, welk aantoont, dat de bomen iets meer als op 16 voeten afstand moeten gesteld worden, als ’t juist in B sal uitkomen; derhalven om de juiste afstand te vinden, so divideer ik de 132 voeten door de voorheen gevondene 8, so komt 16½ voeten voor de juiste distantie tusschen de bomen.’
En bij herhaling: Wat wil ik hier nu mee zeggen? Dat weet ik eigenlijk niet. Ik wilde in ieder geval dat voor mij ‘schurende’ van 1 roede enerzijds en 3,767 meter anderzijds even benoemen.
Jan Holwerda

Uitsnede van kaart van een langwerpig perceel, met de lengte van beide lange zijden en het aantal bomen (1664).

Dan staan er dus 9 bomen met dit sommetje
Klopt Joost. Je hebt een eerste boom en een laatste boom. Daartussen 8 stukken en dus 7 bomen. Levert in het totaal 8 plantafstanden en 9 bomen. Gooi 9 knopen op de keukentafel en ontwerp je laan 🙂
Enige opmerkingen, die niets oplossen, maar die voor mij dan weer belangrijk zijn als je mij naar maten in de Tuinkunst vraagt…
1. Ik weet bijna zeker dat maten die de breedte van een pad of laan of berceau etc. aangeven, nooit vooraf standaard zijn geweest, maar altijd proefondervindelijk werden bepaald. Met z’n drieën door een berceau lopen zal de breedte daarvan gemakkelijk bepalen en de hoogte is weer afhankelijk van de breedte en zeker ook van de beplanting. Je moet je kop niet stoten aan peren in een perenberceau, of aan prik-rozen in een rozenberceau, dus moeten die een beetje hoger zijn dan een kamperfoelie-berceau. Ook de beschikbare financiële middelen spelen een rol en het belang dat de eigenaar hecht aan bepaalde zaken.
2. De Roede is dacht ik al ingesteld in de tijd van Snellius (eerste kwart 17 de eeuw). Het is een maat die afgeleid is van de omtrek van de aarde, vandaar die uiterste precisie. Het is net zoiets als het getal pi, een getal met vele cijfers achter de komma, maar als je iets moet uitrekenen gebruik je er hoogstens 2 Achter de komma. De roede en de voet zijn lengtematen en oppervlaktematen, maar niet specifiek om in de tuinkunst te gebruiken, om plantafstanden vast te stellen!!!! Nu moeten we met cijfers achter de komma werken maar toen natuurlijk niet, want roeden en voeten werden in hele getallen opgegeven (zie op bijgevoegd detail van Jan). Jan van der Groen gaf de plantafstanden voor bomen in roedes op, om ondeskundigen van advies te dienen, maar doorgewinterde tuinlieden wisten precies hoever de diverse bomen uit elkaar moesten staan, afhankelijk van de vorm (dus de wijdte) van de kroon en het gehele bladerdak.
3. Het is gebleken dat tegenwoordig de plantafstanden van bomen vaak groter zijn dan bijvoorbeeld in de 17-de en 18-de eeuw. Is dit een geldkwestie? Om bomen snel omhoog te laten gaan, plant men bomen ook vaak dicht bij elkaar, om een deel later er weer tussen uit te halen, zodat een ruim verdeelde laan ontstaat en men tegelijk hogere bomen heeft om elders aan te planten.
Ik wil maar zeggen, standaarden voor plantafstanden is 1, maar de plantafstanden-praktijk is om welke reden dan ook heel vaak anders.
De roede is geen standaard maat, de Leidse roede is als een zekere standaard overgenomen omdat er geen conventie was in die tijd. De precisie is de omrekening in meters Carla. En met omtrek van de aarde heeft het niets te maken. Wel de zeemijl, die is een boogminuut = 1854 meter op de evenaar, maar op onze breedte ca 1852 meter. In mijn artikel Plantafstanden staan veel van de opmerkingen van Carla verwoord. Dat dicht bij elkaar en daarna er tussentuit halen noemt men ‘blijvers en wijkers’. Dat doet men niet meer, en het heeft het nadeel dat men soms die maatregel van eruit halen na een aantal jaren vergeet. De plantafstand wordt in feite door de ontwerper bepaald, ook vroeger, waarbij het dan gaat om het eindbeeld. Tegenwoordig worden straatbomen verder uiteen geplant omdat men zich meer is gaan realiseren dat de helft van een boom onder grond zit, ofwel de boom moet voldoende grond hebben om tot wasdom te komen maar ook een langer leven.
Over de ‘wijkers en de blijvers’ en andere overwegingen van (een) 18e- en 19e- eeuwse ontwerper heb ik in de laatste CASCADE-uitgave een artikel geschreven. Harmen de Vries en zoon geven een uitgebreide toelichting op hun (of ‘afstand’ vervaardigde) ontwerp voor de Prinsentuin in Leeuwarden (gedateerd 1820). In deze toelichting laten vader en zoon De Vries veel aan het inzicht van de ‘planter’ over, maar ook aan de gegeven omstandigheden in de aanleg zelf.
AvdD
PS: hoe dit uiteindelijk in de praktijk werkte is niet bekend, want het ontwerp van de De Vriesjes werd niet uitgevoerd. Wel dat van Roodbaard; schiet me een vraag te binnen die me al langere tijd bezig houdt: waarom komt de vijvervorm in beide ontwerpen zo sterk overeen? Terwijl De Vries en Roodbaard elkaars werk, waarschijnlijk, niet hebben gezien?
Arinda, kun je dit als separate vraag met uitsneden met beide vijvers aanleveren? 🙂
Beste Joost
geloof me of geloof Wikipedia???
Wat vind ik daar onder Rijnlandse roede?
“De Rijnlandse roede werd op 18 februari 1808 door de Koning van Holland vastgelegd als standaardmaat voor heel Nederland. In 1816 werd het metriek stelsel ingevoerd.”
Dus sinds 1808 wel een standaardmaat.
En verder op Internet over de roede al 200 jaar eerder, is te vinden:
dat Snelleus (in 1615) de omtrek van de aarde uitdrukte in geografische mijlen; elke lengtegraad op de evenaar berekende hij op 15 geografische mijlen. Deze mijl bestond toen uit 1900 Rijnl. roeden. Hij bracht dus de mijl, oftewel een deel van de omtrek van de aarde in verband met de Rijnl. roede.
Het si maar dat jet weet hoe geleerden hier over denken. Ik heb er geen verstand van hoor, maar wist wel dat Snellius er iets mee te maken heeft gehad.