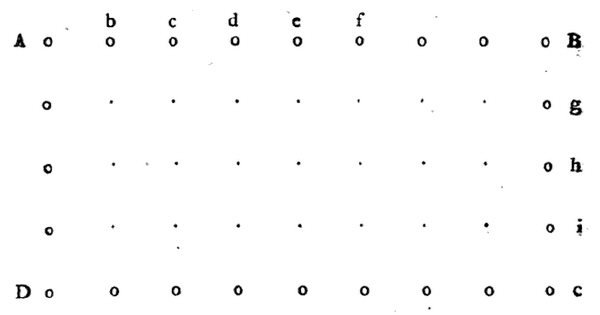
Hoedanig men in het vierkant plant? Uit Beschouwende en werkdadige hovenier-konst (1753), Johann Hermann Knoop

Ik weet niet goed wat ik wil zeggen, hoe het te zeggen, waarom ik het wil zeggen en wat ik er mee wil zeggen. Onduidelijk? Zeker te weten. Volgt een vluchtige zinloze gedachte? Mogelijk.

De titel geeft het veld al aan: plantafstanden. Zie ook eerdere berichten en reacties op onze weblog: 11 nov 2015, 18 juli 2015, 6 jan 2014.

Historische plantafstanden (zeg voor 1820) waren in voeten of roeden, en dan neem ik voor het gemak even de Rijnlandse Roede en laat ik al die anderen en de onderlinge verschillen even achterwege. Laten voor het gemak een plantafstand van 1 roede = 12 voeten = 3,767 meter nemen, en dan noemen we dit ‘standaard’ plantafstand. In meters roept dat aantal cijfers achter de komma roept iets op van dat kan niet, dat doe je niet. Stel je constateert dat een laan een plantafstand van 12 voeten had. Kan iemand zo’n laan herstellen en de bomen op 3,767 m zetten? Lijkt me niet. Ergens botst dat ‘oude’ afgeronde met gemak te gebruiken getal in voeten/roeden met de haast onmogelijke nauwkeurigheid in de ‘nieuwe’ eenheid meters. Terwijl beide tegelijkertijd voor hetzelfde staan. Stel er was nooit sprake geweest van roeden en voeten, maar direct van meters, zou er dan ooit een ‘standaard’ plantafstand van 3,767 m zijn geweest? Denk het niet. Als je bovenstaande doortrekt naar het ontwerp, naar de ontwerptekening, dan doet de maateenheid er waarschijnlijk minder toe. Het gaat dan meer om verhoudingen; 1-2, 3-4 enz.

Wat wil ik hier nu mee zeggen? Dat weet ik eigenlijk niet, heb alleen iets van het ‘schuurt’.

Tot nu gaat het eigenlijk alleen maar over het ideale plaatje, over de ‘standaard’, maar er is ook nog zoiets als het ‘gegevene’, het terrein, met zijn mogelijkheden, beperkingen en onmogelijkheden. En dan kom je tot afwijkingen ten opzichte van de ‘standaard’, of positiever gezegd tot iets als ‘verdeling met benadering van de standaard’. Johann Hermann Knoop geeft een voorbeeld in zijn Beschouwende en werkdadige hovenier-konst (1753). Bij een laan dient eerst de plaats van de eerste (A) en de laatste boom (B) bepaald te worden. De distantie tussen beiden dient vervolgens gemeten te worden: ‘Ik stel B.V. dat de lengte AB 132 voeten was, en dat de bomen circa 16 voeten van malkander sullen staan, dan segt per divisie 16 in de 132 hoeveel maal? Komt 8. Distantie tussen A en B, dat is dat ‘er 9 bomen in die rey komen; maar daar schieten van de 132 voeten 4 voeten over, welk aantoont, dat de bomen iets meer als op 16 voeten afstand moeten gesteld worden, als ’t juist in B sal uitkomen; derhalven om de juiste afstand te vinden, so divideer ik de 132 voeten door de voorheen gevondene 8, so komt 16½ voeten voor de juiste distantie tusschen de bomen.’

En bij herhaling: Wat wil ik hier nu mee zeggen? Dat weet ik eigenlijk niet. Ik wilde in ieder geval dat voor mij ‘schurende’ van 1 roede enerzijds en 3,767 meter anderzijds even benoemen.
Jan Holwerda

Uitsnede van kaart van een langwerpig perceel, met de lengte van beide lange zijden en het aantal bomen (1664).